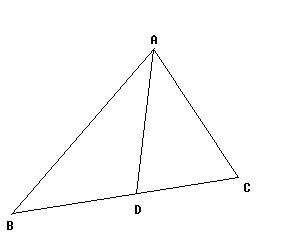
如图,已知AD是△ABC的中线,求证:AB^2+AC^2=2AD^2+2BD^2

来源：学生作业帮编辑：作业帮分类：数学作业时间：2024/11/06 08:50:18

如图,已知AD是△ABC的中线,求证:AB^2+AC^2=2AD^2+2BD^2
那位好心帮帮忙!
余弦定理不会饿、
做AE⊥BC、

作AE⊥BE,根据勾股定理,AB^2=BE^2+AE^2,
AB^2=(BD+DE)^2+AE^2=BD^2+DE^2+2BD*DE+AE^2.(1),
AC^2=CE^2+AE^2=(CD-DE)^2+AE^2=CD^2-2CD*DE+DE^2+AE^2.(2),
BD=CD,
(1)式+(2)式,
AB^2+AC^2=BD^2+CD^2-2BD*DE+2BD*DE+2AE^2+2DE^2
=BD^2+CD^2+2AD^2=2BD^2+2AD^2.
∴AB^2+AC^2=2BD^2+2AD^2.

如图,已知AD是三角形ABC的中线,求证：AB方+AC方=2AD方+2BD方如图,AD是三角形ABC的中线,求证:BC+2AD>AB+AC 已知：如图,△ABC中,AB＞AC,AD是BC边上的高,求证：求证:AB^2-AC^2=BC(BD-DC) 如图,已知:△ABC中,AD是BC边上的中线,试说明不等式AD+BD＞1/2（AB+AC)成立的理由已知AD是三角形ABC的中线,AE是三角形ABD的中线,且AB=BD,求证AC=2AE 如图在三角形abc中,ad是bc边上的中线,求证ad小于2分之1（ab+ac) 已知:如图,在△ABC中,AB>AC,AD是BC边上的高,求证:AB^2-AC ^2=BC (BD -CD ) 如图,已知△ABC,AD是中线,猜想2AD与AB+AC的大小关系,并说明理由. 已知：如图,△ABC中,AD是BC边上的中线,AE是BC边上的高,求证AB²-AC²=2BC×DE上如图,AD是三角形ABC的中线,AE垂直AC,AF垂直AB,且AE=AC,AF=AB,求证：AD=1/2EF 如图,已知：三角形ABC中,AD是BC边上的中线.试说明不等式AD＋BD＞1/2（AB＋AC)成立的理由. 已知：在△ABC中,AD为中线,求证：AD＜1/2（AB+AC)