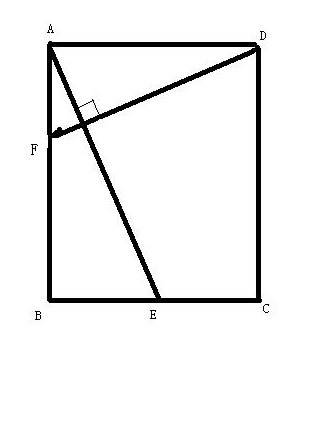
如图,在正方形ABCD中,E是BC边的中点,过D作DF⊥AE交AB于F
如图,在正方形ABCD中,E是BC边的中点,过D作DF⊥AE交AB于F,请你说理
如图:已知正方形ABCD中,E是CD上任意一点,连接AE,过D作DF⊥AE,垂足为N,DF交BC于F,O是AC的中点,连
如图在等腰三角形ABC中,∠ABC=90°,D为AC边上的中点,过D作DE⊥DF,交AB于E,交BC于F.若AE=4,F
如图,在正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC的延长线交于点F,连接EF,与CD边交于点G,与对
如图,已知点E为正方形ABCD的边BC上一点,连接AE,过点D作DG⊥AE,垂足为G,延长DG交AB于点F,若DF=8c
如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D作DE⊥DF,交AB于E,交BC于F,若AE=4,F
如图,在等腰直角三角形abc中角abc等于90°,d为ac的中点,过点d作de垂直df,交ab于点e,交bc于f,若ae
如图11,在等腰三角形ABC中,∠ABC=90,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若AE=4
如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若AE=
如图5,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE
如图,在等腰直角三角形ABC中,∠ABC=90°,点D是AC边上的中点,过点 D作DE⊥DF,交AB于点E,交BC于点F
如图,△ABC中,D是BC的中点,过D点的直线GE交AC于E,交AC的平行线BG于G点,作DF⊥DE交AB于点F,连接E