在直角梯形ABCD中,AD∥BC,AB,⊥BC,∠BCD与∠ADC的角平分线交于AB上的一点,以AB为直径画圆,圆与CD
来源:学生作业帮 编辑:作业帮 分类:数学作业 时间:2024/11/08 17:49:17
在直角梯形ABCD中,AD∥BC,AB,⊥BC,∠BCD与∠ADC的角平分线交于AB上的一点,以AB为直径画圆,圆与CD有
怎样的位置关系?
怎样的位置关系?
精确地画一张图就可以知道,圆与CD相切.
证明:
设角平分线的交点为O,由于∠ADC和∠BCD互为补角,所以∠ODC和∠OCD互为余角,进而证明∠COD=90°.
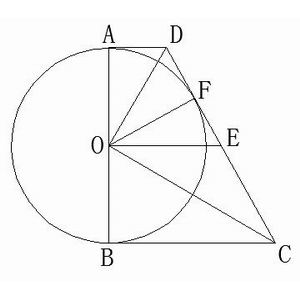
作△COD斜边上的中线OE,即DE=CE,则OE=CE,进而∠EOC=∠ECO=∠BCO(内错角相等),所以OE∥BC.而E是CD中点,所以O必然是AB中点.以AB为直径画圆,圆心一定是O点.
作OF⊥CD,则∠DOF=∠DOC(都跟∠ODC互为余角),而∠AOD=∠BOC(都跟∠BOC互为余角),∠BOC=∠DOC,最终证明∠DOF=∠AOD.再加上∠OAD=∠OFD=90°,OD是公共边,证明△OAD≌△OFD,进而证明OA=OF.这样,以AB为直径(即以OB为半径)的圆一定过点F,即OF是圆O的一条半径.而OF⊥CD,证明圆O与CD相切.
证明:
设角平分线的交点为O,由于∠ADC和∠BCD互为补角,所以∠ODC和∠OCD互为余角,进而证明∠COD=90°.
作△COD斜边上的中线OE,即DE=CE,则OE=CE,进而∠EOC=∠ECO=∠BCO(内错角相等),所以OE∥BC.而E是CD中点,所以O必然是AB中点.以AB为直径画圆,圆心一定是O点.
作OF⊥CD,则∠DOF=∠DOC(都跟∠ODC互为余角),而∠AOD=∠BOC(都跟∠BOC互为余角),∠BOC=∠DOC,最终证明∠DOF=∠AOD.再加上∠OAD=∠OFD=90°,OD是公共边,证明△OAD≌△OFD,进而证明OA=OF.这样,以AB为直径(即以OB为半径)的圆一定过点F,即OF是圆O的一条半径.而OF⊥CD,证明圆O与CD相切.

如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD与∠ADC的平分线于AB上的一点E,以AB为直径做圆
如图,在直角梯形ABCD中,AB⊥AD,AB⊥BC,∠BCD与∠ADC的平分线相交于AB上的一点E,以AB为直径作圆,则
在直角梯形ABCD中,AB垂直于CD,AB垂直于BC,角BCD与角ADC的平分线相交于AB上一点E,以AB为直径作图,则
如图,在直角梯形ABCD中,AB垂直于AD,AB垂直于BC,∠BCD与∠ADC的平分线相交于AB上
在直角梯形ABCD中,AB⊥AD,AB⊥BC,CD=AD+BC.求证以DC为直径的圆O与AB相切.
如图,在直角梯形ABCD中,AB⊥BC,AD∥BC,∠ADC与∠BCD的平分线的交点E落在AB上,求证:AE=DE
直角梯形ABCD中,角A=角B=90°,AD‖BC,E为AB上一点,DE平分角ADC,CE平分角BCD,以AB为直径的圆
在直角梯形abcd中,角A=角B=90度,AD平行于BC,AD+BC=CD.以CD为直径的圆与AB相切吗?为什么?
如图,直角梯形ABCD中,AB=7,∠B=90°,BC-AD=1,以CD为直径的圆与AB相交于两点E,F,且AE=1,在
如图,在梯形ABCD中 AB垂直AD CD垂直AD 且AB+CD=BC 求证 以BC为直径的圆0 与AD相切
如图,直角梯形ABCD中,AD平行BC,CD=AD+BC,试判断以CD为直径的圆与直线AB的位置关系如何?
在梯形ABCD中,CD平行AB,AD=BC,以腰AD为直径的圆O与腰BC相切于G,与底AB相交于E,过E作EF⊥BC,垂