如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,PA=AB,∠ABC=60°,E、F分别是PB,C
来源:学生作业帮 编辑:作业帮 分类:综合作业 时间:2024/11/09 06:18:32
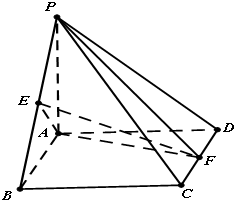 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,PA=AB,∠ABC=60°,E、F分别是PB,CD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,PA=AB,∠ABC=60°,E、F分别是PB,CD的中点.(Ⅰ)证明:PB⊥面AEF
(Ⅱ)求二面角A-PE-F的大小.
(I)证明:∵PA=AB,E是PB的中点,∴PB⊥AE,
∵ABCD是菱形,∠ABC=60°,∴△ABC,△ACD是等边三角形,(1分)
∵F是CD的中点,∴AF⊥CD,
∵AB∥CD,∴AF⊥AB,(2分)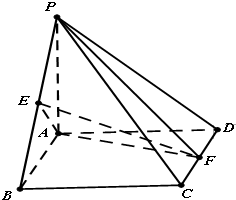
∵PA⊥面ABCD,∴PA⊥AF,
AF∩PA=A,∴AF⊥面PAB,(3分)
PB⊂面PAB,∴AF⊥PB,(4分)
∵AE∩PA=A,∴PB⊥平面 AEF.(5分)
(II)由(I)知,∠AEF是二面角A-PE-F的平面角,(7分)
设AB=a,则AE=
2
2a,AF=
3
2a,(9分)
在Rt△AEF中,tan∠AEF=
6
2,
二面角A-PE-F的大小为arctan
6
2.(10分)
∵ABCD是菱形,∠ABC=60°,∴△ABC,△ACD是等边三角形,(1分)
∵F是CD的中点,∴AF⊥CD,
∵AB∥CD,∴AF⊥AB,(2分)

∵PA⊥面ABCD,∴PA⊥AF,
AF∩PA=A,∴AF⊥面PAB,(3分)
PB⊂面PAB,∴AF⊥PB,(4分)
∵AE∩PA=A,∴PB⊥平面 AEF.(5分)
(II)由(I)知,∠AEF是二面角A-PE-F的平面角,(7分)
设AB=a,则AE=
2
2a,AF=
3
2a,(9分)
在Rt△AEF中,tan∠AEF=
6
2,
二面角A-PE-F的大小为arctan
6
2.(10分)
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点
已知四棱锥p-abcd中,底面abcd为菱形pa⊥平面abcd,∠abc=60度,e,f分别是bc,pc的中点
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且P
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,点M,N分别为BD,PA的中点,
如图,在四棱锥P-ABCD中,底面ABCD是矩形,且PA⊥平面ABCD,AP=AB,BP=BC=2,E、F分别是PB,P
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,E、F分别为BC、P
如图,在四棱锥P-ABCD中,底面ABCD是矩形,且PA⊥平面ABCD,AP=AB,BP=BC=根号2,E、F分别是PB
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AB=√6,点E是棱PB中点
已知四棱锥p-ABCD,底面ABCD为菱形,PA垂直平面ABCD,角ABC=60°,E.F分别是BC.PC的中点.(1)