（1）如图1，已知AC⊥AB，DB⊥AB，AC=BE，AE=BD，试猜想线段CE与DE的大小与位置关系，并证明你的结论．

来源：学生作业帮编辑：作业帮分类：数学作业时间：2024/11/08 14:06:42

（1）如图1，已知AC⊥AB，DB⊥AB，AC=BE，AE=BD，试猜想线段CE与DE的大小与位置关系，并证明你的结论．
（2）如图2，等腰Rt△ABC中，∠ACB=90°．直线DE经过△ABC内部，AD⊥DE于点D，BE⊥DE于点E，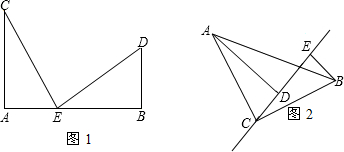

试猜想线段AD、BE、DE之间满足什么关系？证明你的结论．

（1）CE=DE，CE⊥DE．
理由如下：∵AC⊥AB，DB⊥AB，
∴∠A=∠B=90°，
在△ACE和△BED中，
∵

AC＝BE
∠A＝∠B＝90°
AE＝BD，
∴△ACE≌△BED（SAS），
∴CE=DE，∠C=∠BED，
∵∠C+∠AEC=90°，
∴∠BED+∠AEC=90°，
∴∠CED=180°-90°=90°，
∴CE⊥DE；
（2）AD=BE+DE．
理由如下：
∵等腰Rt△ABC中，∠ACB=90°，
∴AC=BC，∠ACD+∠BCE=90°，
∵AD⊥DE于点D，
∴∠ACD+∠CAD=90°，
∴∠CAD=∠BCE，
∵AD⊥DE于点D，BE⊥DE于点E，
∴∠ADC=∠BEC=90°，
在△ACD和△CBE中，
∵

∠CAD＝∠BCE
∠ADC＝∠BEC＝90°
AC＝BC，
∴△ACD≌△CBE（SAS），
∴AD=CE，CD=BE，
∵CE=CD+DE，
∴AD=BE+DE．

（1）如图1，已知AC⊥AB，DB⊥AB，AC=BE，AE=BD，试猜想线段CE与DE的大小与位置关系，并证明你的结论．如图,已知CA⊥AB,DB垂直AB,AC=BE,AE=BD.试猜想线段CE与DE的关系.并说明你的结论. 如图,已知CA⊥ AB,DB⊥AB,AC=BE,AE=BD．试猜想线段CE与DE关系,并说明理由．如图,AB⊥BD,AB‖DE,AB=CD,AC=CE,那么BC与DE有怎样的数量关系?写出你的猜想并已知,如图,AB=AD,AC=AE,∠1=∠2,猜想∠1与∠3的大小关系,并证明你的猜想已知：如图,AB=AD,AC=AE,∠1=∠2,猜想∠1与∠3的大小关系,并证明你的猜想. 如图，已知D是△ABC的边AB上一点，CE∥AB，DE交AC于点O，且OA=OC，猜想线段CD与线段AE的大小关系和位置如图,已知AB//CD,∠1=∠F,∠2=∠E,试猜想AF与DE的位置关系,并证明你的结论. 如图,AB⊥BD,ED⊥BD,AB=CD,BC=DE,则AC与CE的位置关系怎样,写出你的猜想,并说明理由如图,AE⊥AB,AD⊥AC,AB=AE,∠B=∠E,猜想BD与CE的位置关系,说明理由. 已知AB=AC,DB=DE,∠BAC=∠BDE=α．（1）如图1,α=60°,探究线段CE与AD的数量关系,并加以证明如图,已知AB⊥BD与点B,ED⊥BD与点D,且AB=CD,BC=DE,那么AC与CE有什么关系,写出你的猜想,并说明理