matlab大神有空的话帮我看看这个问题,呵呵
来源:学生作业帮 编辑:作业帮 分类:综合作业 时间:2024/11/05 18:50:22
matlab大神有空的话帮我看看这个问题,呵呵
其实这个问题比较简单:在给定区间范围内绘制v=f(z,n)的曲面,公式是现成的,用meshgrid生成区域的座标点,然后代入公式计算,最后用mesh或surf之类的函数绘图即可.
唯一的问题是,v不仅是z和n的函数,还有一个自变量x.但x并非真正的独立变量,而是受另外两个三元方程约束的,对于给定的z,可以用question/577643560.html中的方法求出对应的x来.
你在空间贴出的代码是上述问题中的第一种方法.如果是用Maple内核的MATLAB(例如6.5或2007b,这两个版本上我做了测试),应考虑使用第二种方法,精度更高.
以下是代码,供参考(已作为附件上传):
% 绘图座标范围
ni = linspace(2, 100, 20);
zi = linspace(1, 20000, 30);
% 对于给定的z,求解对应的x
syms x y z
eq1=-2.*pi.*0.05415.*0.0000002.*sin(x).*sin((5.*pi./6)+x)-4./3.*pi.* ...
0.0000002.^3.*2000.*z.*9.8+2./3.*pi.*z.*9.8.*0.0000002.^3.* ...
(1820-1000).*(cos(x)).^3-2./3.*pi.*z.*9.8.*0.0000002.^3.* ...
(1820+1000)-pi.*z.*9.8.*0.0000002.^2.*(y+0.0000002.*cos(x)).* ...
(1820-1000).*(sin(x)).^2;
eq2=-sin((5.*pi./6)+x).*besselk(0,(z.*9.8.*(1820-1000)./0.05415).^ ...
0.5.*0.0000002.*sin(x))+(z.*9.8.*(1820-1000)./0.05415).^0.5.* ...
y.*besselk(1,(z.*9.8.*(1820-1000)./0.05415).^0.5.*0.0000002.*sin(x));
xi = sym( zi*0 );
yi = xi;
for i = 1 : length(zi)
z0 = zi(i);
[xi(i), yi(i)] = solve(subs(eq1,z,z0), subs(eq2,z,z0));
end
% SOLVE的求解结果x位于要求的坐标范围之外,将其减小2*pi并转为数值类型
xi = double(xi-2*pi);
% 计算函数值
[n, z] = meshgrid(ni, zi);
[n, x] = meshgrid(ni, xi);
v = 2*0.05415*(-tan(5*pi/6+x-pi)./(((z*9.8*(1820-1000)/0.05415) ...
.^0.5).*besselk(1,((z*9.8*(1820-1000)/0.05415).^0.5)*0.0000002 ...
.*sin(x)))).^2.*((z*9.8*(1820-1000)/0.05415).^0.5).*besselk(1, ...
((z*9.8*(1820-1000)/0.05415).^0.5)*0.0000002.*n).*(1-1/3.* ...
n.^-1+n.^-3-15/4.*n.^-4-4.46/1000.*(n-1.7).^-2.867)./(3*0.8937 ...
/1000*0.0000002*1.0);
% 绘制曲面及标注图形
mesh(n, z, v)
view(30,15)
xlabel('n')
ylabel('z')
zlabel('v')
曲面效果如下图所示.
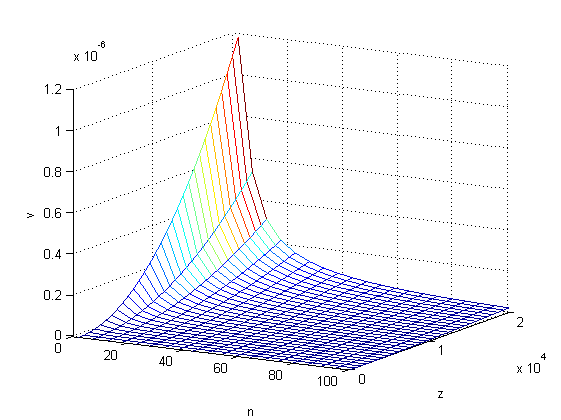
唯一的问题是,v不仅是z和n的函数,还有一个自变量x.但x并非真正的独立变量,而是受另外两个三元方程约束的,对于给定的z,可以用question/577643560.html中的方法求出对应的x来.
你在空间贴出的代码是上述问题中的第一种方法.如果是用Maple内核的MATLAB(例如6.5或2007b,这两个版本上我做了测试),应考虑使用第二种方法,精度更高.
以下是代码,供参考(已作为附件上传):
% 绘图座标范围
ni = linspace(2, 100, 20);
zi = linspace(1, 20000, 30);
% 对于给定的z,求解对应的x
syms x y z
eq1=-2.*pi.*0.05415.*0.0000002.*sin(x).*sin((5.*pi./6)+x)-4./3.*pi.* ...
0.0000002.^3.*2000.*z.*9.8+2./3.*pi.*z.*9.8.*0.0000002.^3.* ...
(1820-1000).*(cos(x)).^3-2./3.*pi.*z.*9.8.*0.0000002.^3.* ...
(1820+1000)-pi.*z.*9.8.*0.0000002.^2.*(y+0.0000002.*cos(x)).* ...
(1820-1000).*(sin(x)).^2;
eq2=-sin((5.*pi./6)+x).*besselk(0,(z.*9.8.*(1820-1000)./0.05415).^ ...
0.5.*0.0000002.*sin(x))+(z.*9.8.*(1820-1000)./0.05415).^0.5.* ...
y.*besselk(1,(z.*9.8.*(1820-1000)./0.05415).^0.5.*0.0000002.*sin(x));
xi = sym( zi*0 );
yi = xi;
for i = 1 : length(zi)
z0 = zi(i);
[xi(i), yi(i)] = solve(subs(eq1,z,z0), subs(eq2,z,z0));
end
% SOLVE的求解结果x位于要求的坐标范围之外,将其减小2*pi并转为数值类型
xi = double(xi-2*pi);
% 计算函数值
[n, z] = meshgrid(ni, zi);
[n, x] = meshgrid(ni, xi);
v = 2*0.05415*(-tan(5*pi/6+x-pi)./(((z*9.8*(1820-1000)/0.05415) ...
.^0.5).*besselk(1,((z*9.8*(1820-1000)/0.05415).^0.5)*0.0000002 ...
.*sin(x)))).^2.*((z*9.8*(1820-1000)/0.05415).^0.5).*besselk(1, ...
((z*9.8*(1820-1000)/0.05415).^0.5)*0.0000002.*n).*(1-1/3.* ...
n.^-1+n.^-3-15/4.*n.^-4-4.46/1000.*(n-1.7).^-2.867)./(3*0.8937 ...
/1000*0.0000002*1.0);
% 绘制曲面及标注图形
mesh(n, z, v)
view(30,15)
xlabel('n')
ylabel('z')
zlabel('v')
曲面效果如下图所示.
