如图,梯形ABCD中,AD平行BC,AB=CD,对角线AC、BD相交于O,AC垂直BD,AD+BC=4cm
来源:学生作业帮 编辑:作业帮 分类:数学作业 时间:2024/11/06 07:06:42
如图,梯形ABCD中,AD平行BC,AB=CD,对角线AC、BD相交于O,AC垂直BD,AD+BC=4cm
求:1)对角线AC的长.
2)梯形ABCD的面积.
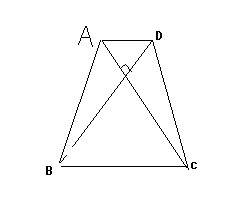
求:1)对角线AC的长.
2)梯形ABCD的面积.

过D作AC的平行线交BC的延长线于点E
∵梯形ABCD中,AD‖BC,AB=CD
∴AC=BD(等腰梯形的两条对角线相等)
∵AD‖BC,
∴AD‖CE,
∴四边形ACED是平行四边形(定义)
∴DE=AC(平行四边形的对边相等)
∵BD⊥AC(已知)
∴BD∴DE
∴△DBE是一个等腰Rt△
过D作DF⊥BE于F
∴F为BE的中点(等腰三角形性质)
∴DF=BF=EF
=BE/2(Rt△斜边中线等于斜边的一半)
∵AD=CE(平行四边形对边相等)
AD+BC=4(已知)
∴BE=4,DF=BF=EF=2
由勾股定理可求AC=DE=2(√2)
∵S△DBE=BE×DF÷2=4
∵△ADB与△ECD等底同高
S梯形ABCD=S△DBE=4

∵梯形ABCD中,AD‖BC,AB=CD
∴AC=BD(等腰梯形的两条对角线相等)
∵AD‖BC,
∴AD‖CE,
∴四边形ACED是平行四边形(定义)
∴DE=AC(平行四边形的对边相等)
∵BD⊥AC(已知)
∴BD∴DE
∴△DBE是一个等腰Rt△
过D作DF⊥BE于F
∴F为BE的中点(等腰三角形性质)
∴DF=BF=EF
=BE/2(Rt△斜边中线等于斜边的一半)
∵AD=CE(平行四边形对边相等)
AD+BC=4(已知)
∴BE=4,DF=BF=EF=2
由勾股定理可求AC=DE=2(√2)
∵S△DBE=BE×DF÷2=4
∵△ADB与△ECD等底同高
S梯形ABCD=S△DBE=4

如图,梯形ABCD中,AD平行BC,AB=CD,对角线AC、BD相交于O,AC垂直BD,AD+BC=4cm
如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD相交于O,且AC⊥BD,若AD+BC=42cm.
如图,梯形ABCD中,AD平行于BC,AB=CD,对角线AC、BD相交于O点,且AC垂直于BD,若AD+BC=4倍根号2
已知,如图,梯形ABCD中,AB=CD ,AD∥BC,对角线AC,BD相交于点O,AC垂直BD ,DH垂直BC于H ,E
如图,梯形ABCD中,AB平行CD,AB>CD,AD=BC,对角线AC,BD相交于O,∠AOB=60°
如图9,在等腰梯形ABCD中AD//BC,AB=CD对角线AC,BD相交于点o且AC⊥BD,若AD+BC=4乘根号2cm
如图,在等腰梯形ABCD中,AD||BC,AB=CD,对角线AC垂直BD,AD=4cm,BC=10cm,求梯形ABCD的
如图所示,在等腰梯形ABCD中,AD平行于BC,AB=CD,对角线AC垂直于BD,且AC=10cm,求梯形ABCD的面积
已知如图等腰梯形ABCD中,AB平行CD,AD=BC,AC垂直BD,
如图,梯形ABCD中,AD平行于BC,对角线AC垂直于BD,且AC=5cm,BD=12cm,求中位线的长
已知:如图梯形ABCD中,AD∥BC,AB=CD,AC与BD相交于点O.
如图,在等腰梯形ABCD中,AD平行BC,AB=CD对角线AC⊥BD.且AC=10cm求梯形ABCD的面积