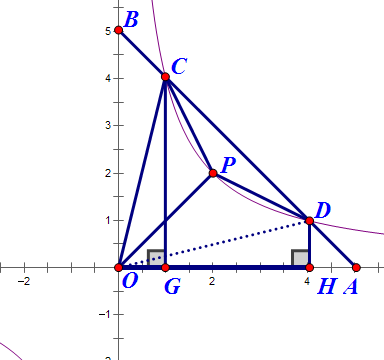
如图,已知C、D是双曲线y=m/x在第一象限内的分支上两点,直线CD分别交x轴、y轴于A、B,CG⊥x轴于G,
来源:学生作业帮 编辑:作业帮 分类:数学作业 时间:2024/11/08 20:43:53
如图,已知C、D是双曲线y=m/x在第一象限内的分支上两点,直线CD分别交x轴、y轴于A、B,CG⊥x轴于G,
DH⊥x轴于H,OG/GC=DH/OH=1/4,OC=根号17
(1)求m的值和D点坐标;
(2)在双曲线第一象限内的分支上是否有一点P,使得S△POC=S△POD?若存在,求出P点坐标;若不存在,请说明理由;
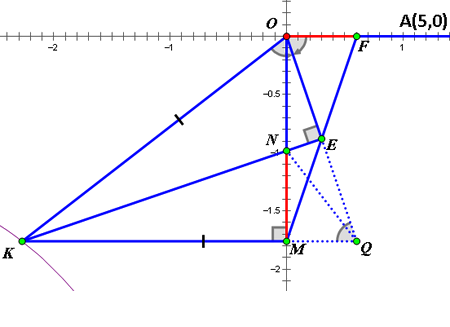
(3)如图2,点K是双曲线y=m/x在第三象限内的分支上的一动点,过点K作KM⊥y轴于M,OE平分∠KOA,KE⊥OE,KE交y轴于N,直线ME交x轴于F,求OF²+MN²/ON²的值
求详解...很急啊...有没有人会
DH⊥x轴于H,OG/GC=DH/OH=1/4,OC=根号17
(1)求m的值和D点坐标;
(2)在双曲线第一象限内的分支上是否有一点P,使得S△POC=S△POD?若存在,求出P点坐标;若不存在,请说明理由;
(3)如图2,点K是双曲线y=m/x在第三象限内的分支上的一动点,过点K作KM⊥y轴于M,OE平分∠KOA,KE⊥OE,KE交y轴于N,直线ME交x轴于F,求OF²+MN²/ON²的值
求详解...很急啊...有没有人会
帮你答一下吧.
(1)如图
设OG=x,则OG²+GC²=OC²
即x²+(4x)²=17,解得x=1(舍去-1)
∴C(1,4)代入y=m/x
解得m=4
连接OD
∵OG/GC=DH/OH且DH⊥x轴,CG⊥x轴
∴△OGC∽△DHO
同时S△OGC=S△DHO(反比例函数性质)
∴△OGC≌△DHO
∴DH=1,OH=4
即D(4,1)
(2)
∵C(1,4)、D(4,1)
∴C、D关于直线y=x对称
P为y=x与y=4/x的交点
联立y=4/x、y=x,
解得P(2,2)[舍去(-2,-2)]
(3)如下图
延长OE、KM交于Q,连接NQ
∵KM⊥y轴,∴∠KQO=∠AOQ=∠KOQ
∴KQ=KO、OE=EQ
即KE是OQ中垂线,∴ON=QN
易证△OEF≌△QEM,∴MQ=OF
在Rt△MNQ中,QN²=MQ²+MN²
即ON²=OF²+MN²
∴(OF²+MN²)/ON²=1
如图,已知C、D是双曲线y=m/x在第一象限内的分支上两点,直线CD分别交x轴、y轴于A、B,CG⊥x轴于G,
如下图,已知C,D是双曲线y=m/x在第一象限内的分支上的两点,直线CD分别交x轴,y轴于A,B两点,设C,D的坐标
如图,C,D是双曲线y=k/x在第一象限内的分支上的两点,直线CD分别交x轴,y轴于A,B两点,设C,D的坐标分别是(x
如图3,C、D两点是双曲线y=k/x在第一象限内的分支上的两点,直线CD分别交X轴、y轴于A、B两点,设C、D的坐标分别
已知C,D是双曲线y=m/x在第一象限内的分支上的两点,直线CD分别交x轴、y轴于A、B两点,
已知C,D是双曲线y=m/x在第一象限分支上的两点,直线CD分别交x轴,y轴于
C.D两点是双曲线y=k/x在第一象限内的分支上的两点 直线CD.分别叫X轴 y轴于A.B两点&nb
cd是双曲线y等于x分之k在第一象限内分之上的两点,直线cd分别交x轴y轴于ab两点,设c,d的坐标分别是(x1,y1)
已知,如图,直线y=32x+92与x轴、y轴分别相交于A、B两点,与双曲线y=kx在第一象限内交于点C,S△AOC=9.
已知,如图,直线y=32x+3与x轴、y轴分别相交于A、B两点,与双曲线y=kx在第一象限内交于点C,且S△AOC=9.
如图,已知直线L:y=3/4x+6分别交x轴、y轴于AB两点,C为直线L上一点,点C在第一象限,过C作CD⊥x轴于D.
如图,直线y=1/2x+2分别于x轴、y轴交于A、C两点,P是该直线在第一象限内的一点,PB⊥x轴.B为垂足.