△ABC中M是AB的中点且向量AN=1/2向量NC,BN与NC相交于点E,设向量AB=a 向量AC=b,试用a,b表示向

来源：学生作业帮编辑：作业帮分类：数学作业时间：2024/11/05 05:30:29

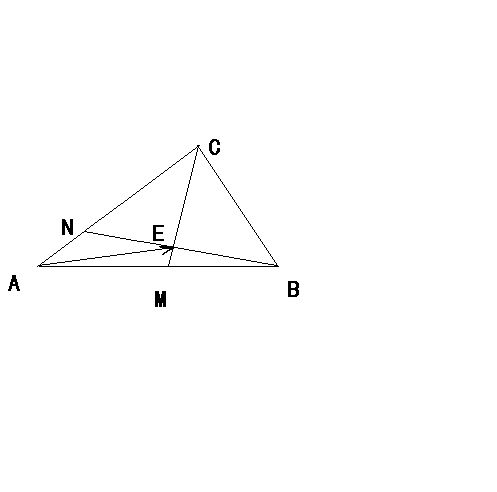
△ABC中M是AB的中点且向量AN=1/2向量NC,BN与NC相交于点E,设向量AB=a 向量AC=b,试用a,b表示向量AE、

怎么证明

设 AE=xa+yb ,
则 AE=xAB+yAC=xAB+3yAN ,由于 B、E、N 三点共线,
所以 x+3y=1 ,-------------（1）
同理,由 AE=xAB+yAC=2xAM+yAC 得 2x+y=1 ,-----------（2）
以上两式解得 x=2/5,y=1/5 ,
即 AE=2/5*a+1/5*b .
再问：则 AE=xAB+yAC=xAB+3yAN ，由于 B、E、N 三点共线 X+3Y=1 怎么来的
再答：这是三点共线的充要条件。 P 在直线 AB 上的充要条件是：存在实数 λ ，使得对平面内任一点 O ，有 OP=λOA+(1-λ)OB 。这个结论在高中课本中，是一道例题，里面有详细的证明。

△ABC中M是AB的中点且向量AN=1/2向量NC,BN与NC相交于点E,设向量AB=a 向量AC=b,试用a,b表示向三角形ABC中,M为AB中点,N为AC上一点,且AN/NC=1/2,BN与CM相交于E,设AB向量=a,AC向量=b,试三棱锥S-ABC中,M为AB的中点,N在BC上,且BN:NC=2:1,AN与CM交于点O,设向量SA=向量a,SB=b, 在三角形ABC中,点M是BC的中点,点N在AC的边上,且向量AN=2NC,AM与BN相交于点P,求向量AP比向量PM的值平行四边形ABCD中,向量AB=a,向量AD=b,向量AN=3倍向量NC,M为BC的中点,则向量MN=? 在三角形ABC中,点M在BC的中点,点N在边AC上,且AN=2NC,AM与BN相交于点P,求向量AP比向量PM的值. 在三角形ABC中,D为BC的中点,已知AB=向量a,AC=向量b,（1）试用向量a,向量b表示向量AD. 在平行四边形ABCD中,向量AB=a,向量AD=b,向量AN=3向量NC,M为BC中点,则向量MN=? 已知在三角形ABC中,M与N分别为AB与AC的中点,且向量AB=向量a,向量AC=向量b,用向量a,向量b表示如下向量：在平行四边形ABCD中,向量NC=三分之一向量AN,M为BC的中点,设向量AB=a,向量AD=b,以a,b为基底,则向量若三角形ABC中,AM=1/3AB,AN=1/4AC,BN与CM交于点P,且向量AB=a,向量AC=b,用a,b表示向量 △ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量AB=向量a,向量AC=向量b