（2013•松北区三模）如图，直线y=-2x+5分别与x、y轴交于点A、B，经过点C（-2，0）的直线y=x+b与y轴交

来源：学生作业帮编辑：作业帮分类：综合作业时间：2024/11/09 10:41:12

（2013•松北区三模）如图，直线y=-2x+5分别与x、y轴交于点A、B，经过点C（-2，0）的直线y=x+b与y轴交于点D，且直线AB、CD交于点E．
（1）求点E的坐标．
（2）点Q（m，n）为线段AB上一点（与点E不重合），QM∥x轴，交直线CE于点M，设线段QM的长为d，写出d与m的函数关系式（直接写出相应m的取值范围）．
（3）在（2）的条件下，点E关于直线QM的对称点为F，当BFC=90°时，求点M的坐标．

（1）∵直线y=x+b经过点C（-2，0）
∴0=-2+b    b=2
由

y＝−2x+5
y＝x+2 得

x＝1
y＝3
∴E（1，3）；

（2）∵点Q（m，n）为线段AB上一点，
∴n=-2m+5
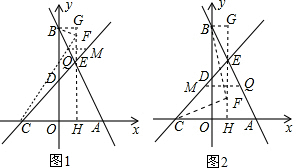
如图1，当点Q在BE上时，即0＜m＜1
∵QM∥x轴∴点M的纵坐标为n，将y=n代入y=x+2=n
解得：x=n-2
∴M（n-2，n）
QM=n-2-m=-2m+5-2-m=-3m+3（0＜m＜1）；
如图2，当点Q在AE上时，即1＜m＜2.5
QM=3m-3（1＜m＜2.5）．

（3）如图，过点F作GH⊥x轴于点H，作BG⊥GH于点G．
∵△BGH∽△FHC
∴BG：FH=GF：CH
∵点E、点F关于直线QM的对称，
∴设F（1，k）则BG=1，GF=5-k，FH=k，CH=3
1：k=（5-k）：3   即k²-5k+3=0
解得：k=
5±
13
2
n=

5±
13
2+3
2=
11±
13
4

（2013•松北区三模）如图，直线y=-2x+5分别与x、y轴交于点A、B，经过点C（-2，0）的直线y=x+b与y轴交如图,已知直线y=x-2与x轴、y轴分别交于点A和点B,另一直线y=kx+b与y轴交于点C（0,7）如图,已知直线y=-x+2与x轴、y轴分别交于点A和点B,另一直线y=kx+b（k不等于0）经过点C（1,0）,且把三角如图,已知直线y=-x+2与x轴,y轴分别交于点A和点B,另一直线y=kx+b(k≠0)经过点C（1,0）,且把△AOB 如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C（1,a）是直线与双曲线如图,已知直线y=-x+2与x轴、y轴分别交于点A和点B,另已知直线y= kx+b(k≠0)经过点C 如图,已知直线y=x+6与x轴,y轴分别交于点A,B,另一条直线y=kx+b（k,b为常数,k≠0）经过点C（-3,0）如图,直线y=-（4/3）x+4与x轴交于点A与y轴交于点C,已知二次函数的图像经过点A、C和点B(-1,0) （2014•松北区一模）如图，抛物线y=-x2+bx+c与直线y=12x+2交于C、D两点，其中点C在y轴上，点D的坐标如图（有图）,直线y=-2x+8与X轴分别交于点A、B,抛物线y=ax^2+bx（a≠0）经过点A,顶点M在直线y=-2 如图,直线l1:y=-x+b与x轴交于点A,与y轴交于点B,与直线l2:y=-2x交于点（m,6）已知：如图,直线y=-2x+4的图像与x轴,y轴分别交于A、B两点另外一条直线L经过（-1,0）,与线段A、B交于C,并